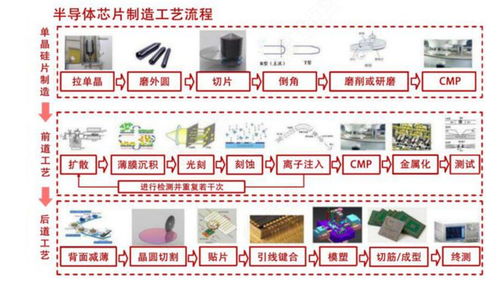
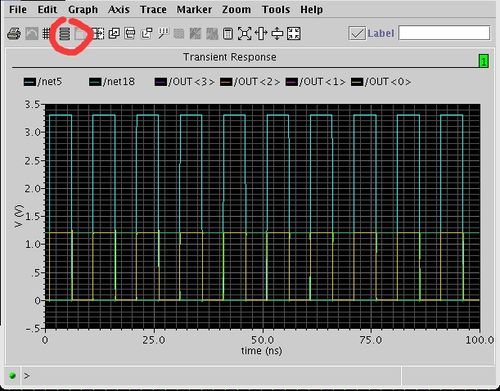
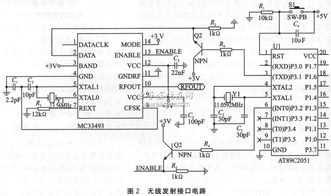
集成運算放大器構成的運算電路分析與功能探究

在集成電路設計中,集成運算放大器(簡稱運放)是構成各種模擬信號處理電路的核心元件。本文將以一個典型的由運放構成的運算電路為例,詳細推導其輸入輸出之間的關系,并深入分析該電路所實現的運算功能。\n\n### 一、電路結構與基本假設\n\n假設電路為經典的反相比例運算電路或同相比例運算電路,這是兩種最基礎且應用最廣泛的運放電路拓撲。為進行一般性分析,我們基于以下理想運放條件:\n1. 開環電壓增益無窮大。\n2. 輸入阻抗無窮大。\n3. 輸出阻抗為零。\n4. 輸入失調電壓、輸入偏置電流等非理想因素為零。\n\n### 二、輸入輸出關系推導\n\n以最典型的反相比例運算電路為例進行推導。該電路結構為:輸入電壓 \( V{in} \) 通過一個輸入電阻 \( R1 \) 連接到運放的反相輸入端(-)。運放的同相輸入端(+)通過一個電阻 \( R3 \) 接地(通常 \( R3 \) 用于平衡偏置電流,其值等于 \( R1 \) 與反饋電阻 \( Rf \) 的并聯值,但在理想分析中常直接接地)。在反相輸入端與輸出端 \( V{out} \) 之間連接有反饋電阻 \( Rf \)。\n\n根據理想運放“虛短”(兩輸入端電位相等)和“虛斷”(流入兩輸入端的電流為零)的特性:\n1. 由于同相輸入端接地,反相輸入端電位也為零,即“虛地”。\n2. 流過電阻 \( R1 \) 的電流 \( I1 \) 全部流過反饋電阻 \( Rf \),即 \( I1 = If \)。\n\n由此可得:\n\\[ I1 = \\frac{V{in} - 0}{R1} = \\frac{V{in}}{R1} \\]\n\\[ If = \\frac{0 - V{out}}{Rf} = -\\frac{V{out}}{Rf} \\]\n由于 \( I1 = If \),因此:\n\\[ \\frac{V{in}}{R1} = -\\frac{V{out}}{Rf} \\]\n整理得到輸入輸出關系:\n\\[ V{out} = -\\left( \\frac{Rf}{R1} \\right) V{in} \\]\n\n對于同相比例運算電路(輸入電壓 \( V{in} \) 接同相端,反相端通過電阻 \( R1 \) 接地并通過 \( Rf \) 反饋至輸出),采用類似的分析方法可得:\n\\[ V{out} = \\left( 1 + \\frac{Rf}{R1} \\right) V{in} \\]\n\n### 三、電路功能分析\n\n1. 數學運算功能:上述推導明確顯示,這兩種基本電路實現了輸入電壓 \( V{in} \) 與一個常系數(由外部電阻 \( R1 \) 和 \( Rf \) 的比值決定)的乘法運算。反相電路的系數為 \( -Rf/R1 \),輸出與輸入反相;同相電路的系數為 \( 1 + Rf/R1 \),輸出與輸入同相。通過選擇不同的電阻值,可以靈活設置放大倍數(增益)或衰減系數。這是模擬計算機中進行比例、縮放等線性運算的基礎單元。\n\n2. 信號調理功能:在更廣泛的模擬信號處理系統中,此類電路是核心的放大器。通過精確設置電阻網絡,可以設計出特定增益的電壓放大器,用于將微弱的傳感器信號(如熱電偶、應變片、麥克風信號)放大到適合后續電路(如模數轉換器ADC)處理的電平范圍。其高輸入阻抗和低輸出阻抗特性也便于實現級聯和阻抗匹配。\n\n3. 構建模塊功能:此基本運算電路是構建更復雜功能電路的基石。通過增加更多的輸入電阻,可以構成加法器(反相加法電路)。通過與電容組合,可以構成積分器或微分器,實現動態的微積分運算,廣泛應用于波形生成、濾波器和控制系統。通過改變反饋網絡的復雜程度(如引入非線性元件),還能實現對數、指數等非線性運算。\n\n4. 集成電路設計意義:在芯片設計層面,盡管基本運放本身是一個高度集成的器件,但其外圍的電阻網絡(\( R1, R_f \))決定了電路的整體功能。在單片集成電路設計中,這些電阻可以通過晶圓上的薄膜電阻工藝精確實現,從而將整個運算功能(如可編程增益放大器PGA)集成到單一芯片中,實現系統的小型化、高可靠性和低成本批量生產。分析此類電路是理解模擬IP模塊、數據轉換器前端、濾波器和穩壓器等復雜IC子系統工作原理的關鍵第一步。\n\n### 四、結論\n\n由集成運算放大器與電阻網絡構成的基本運算電路,其核心功能是實現對輸入電壓的線性比例運算(放大或衰減)。反相與同相兩種配置提供了增益符號和輸入阻抗上的不同選擇。該電路不僅是實現模擬數學運算的基礎單元,更是現代電子系統中不可或缺的信號調理與放大模塊。深入理解其輸入輸出關系及工作原理,是進行模擬集成電路與系統設計、分析和應用的重要基礎。
如若轉載,請注明出處:http://m.camker.cn/product/52.html
更新時間:2026-01-07 04:11:38